27. Gauss' Theorem
Let \(V\) be a nice solid region in \(\mathbb{R}^3\) with a nice properly oriented boundary, \(\partial V\), and let \(\vec F\) be a nice vector field on \(V\). Then \[ \iiint_V \vec\nabla\cdot\vec F\,dV =\iint_{\partial V} \vec F\cdot d\vec S \] The outer boundary must be oriented outward while any inner boundaries must be oriented inward. This means that all pieces of the boundary are oriented away from the solid.
d. Applications
5. Gauss' Law
Gauss' Law is a law of physics relating electric charge to the electric field. It can be written in a differential or integral version, which are related by Gauss' Theorem. The differential version states that the divergence of the electric field is equal to \(4\pi\) times the electric charge density \(\delta_e\). The integral version states that the flux of the electric field through a closed surface is equal to \(4\pi\) times the net electric charge \(Q\) contained within the volume whose boundary is the given closed surface. (The coefficient \(4\pi\) may change for other choices of units.)
- Differential version: \(\vec\nabla\cdot\vec E=4\pi\delta_e\)
- Integral version: \(\displaystyle \iint_{\partial V} \vec E\cdot d\vec S =4\pi Q\)
\(\delta_e\) is the electric charge density and \(Q\) is the net electric charge in a solid region \(V\) which can be computed from the integral \(\displaystyle Q=\iiint_V \delta_e\,dV\). And the closed surface \(\partial V\) is the boundary of \(V\).
Prove the differential version of Gauss' Law implies the integral version, using Gauss' Theorem.
Start by applying Gauss' Theorem to the integral \(\displaystyle \iint_{\partial V} \vec E\cdot d\vec S\).
We start by applying Gauss' Theorem to the left side of the integral version of Gauss' Law: \[ \iint_{\partial V} \vec E\cdot d\vec S =\iiint_V \vec\nabla\cdot\vec E\,dV \] Then, we use the differential version of Gauss' Law, \(\vec\nabla\cdot\vec E=4\pi\delta_e\), to get \[ \iint_{\partial V} \vec E\cdot d\vec S =4\pi\iiint_V \delta_e\,dV \] Finally, we use the formula for the net charge as the integral of the charge density \(\displaystyle Q=\iiint_V \delta_e\,dV\) to obtain: \[ \iint_{\partial V} \vec E\cdot d\vec S =4\pi Q \] Thus, we have proven the integral version of Gauss' Law by using Gauss' Theorem and the differential version of Gauss' Law.
In the following example, we will use Gauss' Law to find the charge \(Q\) inside a sphere from the electric field \(\vec E\) in two different ways, once from a volume integral of the density and once from a surface integral over a sphere.
Assume the electric field in a region of space is \[ \vec E=\left\langle \dfrac{x}{(x^2+y^2+z^2)^{1/2}}, \dfrac{y}{(x^2+y^2+z^2)^{1/2}}, \dfrac{z}{(x^2+y^2+z^2)^{1/2}} \right\rangle \]
Compute the total charge inside the sphere of radius \(3\) centered at the origin in two ways.
In spherical coordinates, if \(\vec r=\langle x,y,z\rangle\) then \(|\vec r|=\sqrt{x^2+y^2+z^2}=\rho\) and \(\hat r=\left\langle \dfrac{x}{\rho},\dfrac{y}{\rho},\dfrac{z}{\rho}\right\rangle\). Consequently, \(\vec E=\hat r\), the unit vector in the radial direction as shown in the plot.
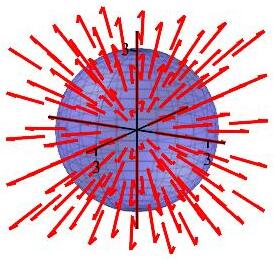
We first find \(\delta_e\) using Gauss' law, and then compute \(Q\) as a volume integral.
To use the differential version of Gauss' Law, we need to find the divergence of \(\vec E\). By the quotient rule, \[\begin{aligned} \dfrac{\partial E_1}{\partial x} &=\dfrac {(x^2+y^2+z^2)^{1/2}\cdot1-x\cdot\dfrac{1}{2}(x^2+y^2+z^2)^{-1/2}2x} {x^2+y^2+z^2 } \\[2pt] &=\dfrac{(x^2+y^2+z^2)-x^2}{(x^2+y^2+z^2)^{3/2}} =\dfrac{y^2+z^2}{(x^2+y^2+z^2)^{3/2}} \end{aligned}\] Similarly \[ \dfrac{\partial E_2}{\partial y} =\dfrac{x^2+z^2}{(x^2+y^2+z^2)^{3/2}} \qquad \text{and} \qquad \dfrac{\partial E_3}{\partial z} =\dfrac{x^2+y^2}{(x^2+y^2+z^2)^{3/2}} \] So \[\begin{aligned} \vec\nabla\cdot\vec E &=\dfrac{y^2+z^2}{(x^2+y^2+z^2)^{3/2}} +\dfrac{x^2+z^2}{(x^2+y^2+z^2)^{3/2}} +\dfrac{x^2+y^2}{(x^2+y^2+z^2)^{3/2}} \\[2pt] &=\dfrac{2(x^2+y^2+z^2)}{(x^2+y^2+z^2)^{3/2}} =\dfrac{2}{\sqrt{x^2+y^2+z^2}} \end{aligned}\] By Gauss' Law, \[ \delta_e=\dfrac{1}{4\pi}\vec\nabla\cdot\vec E =\dfrac{1}{2\pi\sqrt{x^2+y^2+z^2 } }. \] This is the charge density at each point in the sphere. In spherical coordinates, \(\delta_e=\dfrac{1}{2\pi\rho}\). To find the charge, we use spherical coordinates and integrate over the volume \[\begin{aligned} Q&=\iiint_V \delta_e\,dV =\int_0^{2\pi}\int_0^\pi\int_0^3 \dfrac{1}{2\pi\rho} \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\dfrac{1}{2\pi}\int_0^{2\pi} 1\,d\theta \int_0^\pi \sin\phi\,d\phi \int_0^3 \rho\,d\rho \\ &=\left[\rule{0pt}{10pt}-\cos\phi\right]_0^\pi \left[\dfrac{\rho^2 }{2}\right]_0^3 =(1-(-1))\dfrac{9}{2}=9 \end{aligned}\]
Alternatively, use Gauss' Law to find \(\displaystyle Q=\dfrac{1}{4\pi}\iint_{\partial V} \vec E\cdot d\vec S\)
Here the integral is computed over the surface of the sphere parametrized as: \[ \vec R(\phi,\theta) =(3\sin\phi\cos\theta,3\sin\phi\sin\theta,3\cos\phi) \] The normal is: \[ \vec N =\langle 9\sin^2\phi\cos\theta,9\sin^2\phi\sin\theta,9\sin\phi\cos\phi\rangle \] On the sphere, the electric field \(\vec E\) is \[\begin{aligned} \vec E(\vec R(\phi,\theta)) &=\left\langle \dfrac{x}{(x^2+y^2+z^2)^{1/2}}, \dfrac{y}{(x^2+y^2+z^2)^{1/2}}, \dfrac{z}{(x^2+y^2+z^2)^{1/2}} \right\rangle\\ &=\left\langle \dfrac{3\sin\phi\cos\theta}{3}, \dfrac{3\sin\phi\sin\theta}{3}, \dfrac{3\cos\phi}{3}\right\rangle\\ &=\langle \sin\phi\cos\theta,\sin\phi\sin\theta,\cos\phi\rangle \end{aligned}\] Their dot product is: \[\begin{aligned} \vec E\cdot\vec N &=9\sin^3\phi\cos^2\theta+9\sin^3\phi\sin^2\theta+9\sin\phi\cos^2\phi \\ &=9\sin^3\phi+9\sin\phi\cos^2\phi \\ &=9\sin\phi(\sin^2\phi+\cos^2\phi) =9\sin\phi \end{aligned}\] We can now integrate: \[\begin{aligned} \iint_{\partial V} &\vec E\cdot d\vec S =\int_0^{2\pi}\int_0^\pi \vec E\cdot\vec N\,d\phi\,d\theta =\int_0^{2\pi}\int_0^\pi 9\sin\phi\,d\phi\,d\theta\\ &=9(2\pi)\left[\rule{0pt}{10pt}-\cos\phi\right]_0^\pi =18\pi(-(-1)-(-1))=36\pi \end{aligned}\] Finally we use the integral version of Gauss' Law to compute the charge: \[ Q=\dfrac{1}{4\pi}\iint_{\partial V} \vec E\cdot d\vec S= \dfrac{36\pi}{4\pi}=9 \] This agrees with our other method of calculating \(Q\).
The electric field inside a block of semiconductor with dimensions \(0 \le x \le 4\), \(0 \le y \le 3\) and \(0 \le z \le 2\) is \[ \vec E=\langle 3x+5y-4z,x-2y+5z,3x-2y+5z\rangle \] Compute the net charge inside the block in two ways.
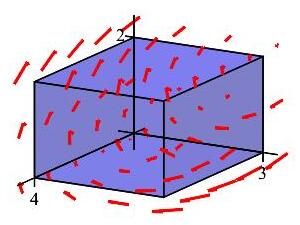
-
Use the differential form of Gauss' Law to find the charge density and integrate to find the net charge.
\(Q=\dfrac{36}{\pi}\)
We use Gauss' Law to find the charge density: \[ \delta_e=\dfrac{1}{4\pi}\vec\nabla\cdot\vec E =\dfrac{1}{4\pi}(3-2+5)=\dfrac{3}{2\pi} \] Then we integrate to get the net charge: \[ Q=\iiint_V \delta_e\,dV =\int_0^2\int_0^3\int_0^4 \dfrac{3}{2\pi}\,dx\,dy\,dz =24\dfrac{3}{2\pi}=\dfrac{36}{\pi} \]
-
Use the integral form of Gauss' Law to find the net charge.
\(Q=\dfrac{36}{\pi}\)
We need to do \(6\) surface integrals. Everything is in rectangular coordinates. Recall: \(\vec E=\langle 3x+5y-4z,x-2y+5z,3x-2y+5z\rangle\)
\(x=0\): The normal is \(\vec N=-\hat\imath\) and its dot product with \(\vec E\) on the surface is \(\vec E\cdot\vec N=-(5y-4z)\). \[ \iint_{x=0} \vec E\cdot d\vec S =-\int_0^2\int_0^3 (5y-4z)\,dy\,dz =-21 \] \(x=4\): The normal is \(\vec N=\hat\imath\) and its dot product with \(\vec E\) on the surface is \(\vec E\cdot\vec N=(12+5y-4z)\). \[ \iint_{x=0} \vec E\cdot d\vec S =\int_0^2\int_0^3 (12+5y-4z)\,dy\,dz =93 \] \(y=0\): The normal is \(\vec N=-\hat\jmath\) and its dot product with \(\vec E\) on the surface is \(\vec E\cdot\vec N=-(x+5z)\). \[ \iint_{y=0} \vec E\cdot d\vec S =-\int_0^2\int_0^4 (x+5z)\,dx\,dz =-56 \] \(y=3\): The normal is \(\vec N=\hat\jmath\) and its dot product with \(\vec E\) on the surface is \(\vec E\cdot\vec N=(x-6+5z)\). \[ \iint_{y=3} \vec E\cdot d\vec S =\int_0^2\int_0^4 (x-6+5z)\,dx\,dz =8 \] \(z=0\): The normal is \(\vec N=-\hat k\) and its dot product with \(\vec E\) on the surface is \(\vec E\cdot\vec N=-(3x-2y)\). \[ \iint_{y=0} \vec E\cdot d\vec S =-\int_0^3\int_0^4 (3x-2y)\,dx\,dy =-36 \] \(z=2\): The normal is \(\vec N=\hat k\) and its dot product with \(\vec E\) on the surface is \(\vec E\cdot\vec N=(3x-2y+10)\). \[ \iint_{y=3} \vec E\cdot d\vec S =\int_0^3\int_0^4 (3x-2y+10)\,dx\,dy =156 \] We add the \(6\) integrals to get the total flux. So the charge is: \[\begin{aligned} Q&=\dfrac{1}{4\pi}\iint_{\partial V} \vec E\cdot d\vec S \\ &=\dfrac{1}{4\pi}(-21+93-56+8-36+156) =\dfrac{36}{\pi} \end{aligned}\] This is the same as part (a).
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum